Acima vimos que um número natural também é um número inteiro (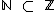 
), assim como um número inteiro também é um número racional ( 
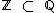), portanto 
.
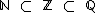Vimos também que os números racionais não estão contidos no conjunto dos números irracionais e vice-versa. A intersecção destes conjuntos resulta no conjunto vazio: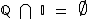 
A intersecção é uma operação por meio da qual obtemos um conjunto de todos os elementos que pertencem simultaneamente a todos os conjuntos envolvidos. Sejam dois conjuntos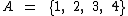 
e 
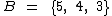, a intersecção entre estes dois conjuntos será 
.
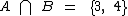O conjunto dos números reais é representado pela letra R (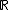 
) e é formado pela união do conjunto dos números racionais com o conjunto dos irracionais, que simbólicamente representamos por: 
.
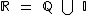A união é uma operação por meio da qual obtemos um conjunto de todos os elementos que pertencem ao menos a um dos conjuntos envolvidos. Sejam dois conjuntos 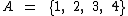e 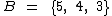, a união entre estes dois conjuntos será 
.
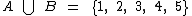O conjunto dos números racionais está contido no conjunto dos números reais (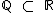 
), assim como o conjunto dos números irracionais também é subconjunto do conjunto dos números reais ( 
).
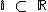Através dos caracteres especiais "+" e "*", por exemplo, podemos representar o conjunto dos números reais positivos por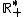 
.
Abaixo temos um exemplo de conjunto contendo número reais:
0 comentários:
Postar um comentário